반응형
직선과 원의 벡터방정식을 구하는 방법을 살펴보자.
직선의 벡터방정식 구하기
하나의 직선은 두개의 점 또는 하나의 점과 기울기로 결정할 수 있다. 따라서 2가지 조건에 따른 직선의 벡터방정식을 구해보자.
1. 점 A를 지나고 →d에 평행한 직선의 방정식

1) 직선의 벡터방정식
점 A와 직선 위의 점을 P라 하면, 위치벡터는 각각 →a,→p 라 하자.
이 때, 직선의 벡터방정식은
→p=→a+t→d (단, t는 실수) 이다.
2) 직선의 방정식
점 A가 (x,y)이고, 방향벡터를 →d=(l,m)이라 하면, 직선의 방정식은
x−x1l=y−y1m (단, l≠0,m≠0) 이다.
2. 두 점 A, B를 지나는 직선의 방정식

1) 직선의 벡터방정식
점 A, B 와 직선 위의 점을 P라 하면, 위치벡터는 각각 →a,→b,→p라 하자.
이때, 직선의 벡터방정식은
→p=→a+t(→b−→a) (단, t는 실수) 이다.
2) 직선의 방정식
점 A, B가 각각 (x1,y1),(x2,y2) 이라 하면, 직선의 방정식은
x−x1x2−x1=y−y1y2−y1 (단, x1≠x2,y1≠y2) 이다.
728x90
'수학' 카테고리의 다른 글
| 벡터에서 내분점, 외분점의 위치벡터 구하는 방법 알아보기 (0) | 2022.11.07 |
|---|---|
| 원과 구의 벡터방정식 구하는 방법 (0) | 2022.11.07 |
| 자연상수 e가 무리수인 이유 알아보기 (0) | 2022.11.07 |
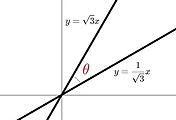
| 직선과 직선 사이의 각 구하는 2가지 방법 알아보기 (0) | 2022.11.07 |
| 삼각형의 넓이를 구하는 공식 모음 (0) | 2022.11.06 |


댓글