방정식이라는 단어는 1세기경에 중국의 '구장산술'이라는 책에서 처음 사용되었다고 알려져있다.
방정식이라는 단어는 방정은 두 수를 비교해 서로 같은 수로 만드는 법을 의미한다.
일차방정식의 역사
일차방정식은 기원전 1650년 경에 11개의 일차방정식 문제가 '린드 파피루스'에 기록되어 있는데, 그 중 가장 오래된 일차방정식 문제는 '아하' 문제이다.
'아하' 문제
'아하' 와 '아하'의 $\frac{1}{7}$ 을 더해서 19일 때, '아하'는 얼마인지 구하시오.
이 문제는 결국 $x+\frac{1}{7}x = 19$라는 일차방정식 문제와 같다.
하지만, 이집트 사람들은 문자를 $x$로 나타내지 못했기 때문에 가정법을 사용해서 문제를 해결하였는데, 당시 문제해결방법은 다음과 같다.
먼저 답을 7이라고 가정하자. 그러면, $7+\frac{1}{7} = 8$ 이다. 이건 답이 아니다. 따라서 8에서 2를 곱하면, 16이고, 8에서 $\frac{1}{4}$을 곱하면, 2이고, 8에서 $\frac{1}{8}$을 곱하면 1 이다. 이를 모두 더하면, $16+2+1 = 19$이다.
이를 이용하면, $7 \times 2 + 7 \times \frac{1}{4} + 7 \times \frac{1}{8} = 14+ \frac{7}{4} + \frac{7}{8} = \frac{133}{8}$ 이다. 즉, '아하' 는 $\frac{133}{8}$ 이다.
디오판토스 묘비 문제
디오판토스(Diophantos) (200~284) 의 묘비에는 그의 일생에 관련된 내용의 방정식 문제가 기록되어 있다. 디오판토스는 몇살에 죽었는지 알아보는 문제를 풀어보자.
디오판토스는 일생의 $\frac{1}{6}$을 어린이로, $\frac{1}{12}$은 청년으로 살았으며, 인생의 $\frac{1}{7}$은 미혼으로 살아왔다. 결혼 후 5년째에 아들을 낳았으며 그 아들은 아버지보다 4년 먼저 죽었다. 그때 죽은 아들의 나이는 아버지의 나이의 절반이다. 그렇다면, 디오판토스는 몇살에 죽었을까요?
풀이
디오판토스의 죽었을 때 나이를 $x$라 하면
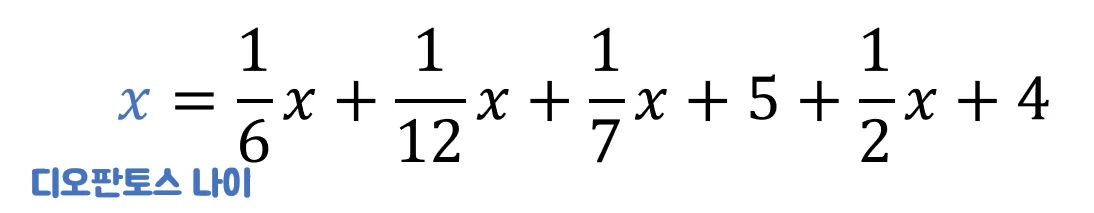
이 일차방정식을 풀면 디오판토스는 84세라는 것을 알 수 있다.
'수학' 카테고리의 다른 글
| 여러가지 함수의 급수 전개 (0) | 2022.12.16 |
|---|---|
| 점화식의 특성다항식 이용해 일반항 구하는 방법 (0) | 2022.12.15 |
| 수학 기호 사용의 역사 (0) | 2022.12.13 |
| 수학에서 문자 사용의 의미 알아보기 (0) | 2022.12.12 |
| 정수의 개념과 정수의 성질 (0) | 2022.12.11 |

댓글