삼각형의 외각의 이등분선 정리
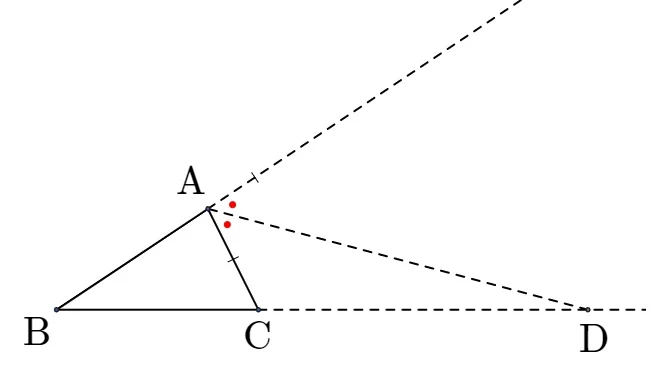
$\bigtriangleup \rm ABC$의 $\angle \rm A$의 외각의 이등분선과 변 $\rm BC$의 연장선과의 교점을 $\rm D$라 할 때,
$\overline{\rm AB} : \overline{\rm AC} = \overline{\rm BD} : \overline{\rm CD}$ 이다.
또한 위의 역 정리 또한 성립한다. 즉, $\bigtriangleup \rm ABC$에서 변 $\rm BC$의 연장선 위의 한 점 $\rm D$에 대하여 $\overline{\rm AB} : \overline{\rm AC} = \overline{\rm BD} : \overline{\rm CD}$가 성립하면, 선분 $\rm AD$는 $\angle \rm BAC$의 외각의 이등분선이다.
증명하기
($\Rightarrow$)
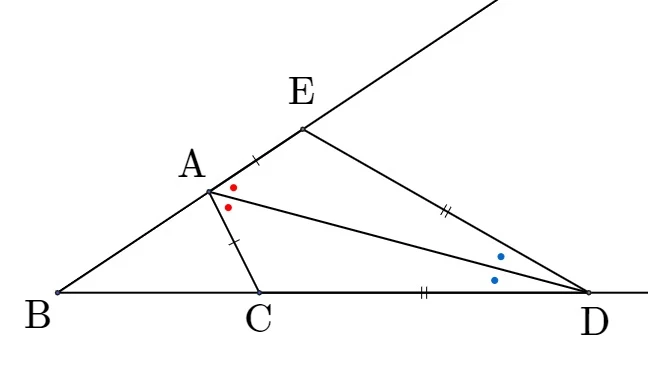
내각의 이등분선에 의해
$\rm D$에서 각의 이등분선을 긋는다. $\rm \bigtriangleup ACD \equiv \bigtriangleup AED$이므로
$\overline{\rm AE} = \overline{\rm AC}$이고, $\overline{\rm CD} = \overline{\rm DE}$ 이다. 따라서
$\overline{\rm AB} : \overline{\rm AE} = \overline{\rm BD} : \overline{\rm DE}$ $\Rightarrow$ $\overline{\rm AB} : \overline{\rm AC} = \overline{\rm BD} : \overline{\rm DC}$ 가 성립한다.
($\Leftarrow$)
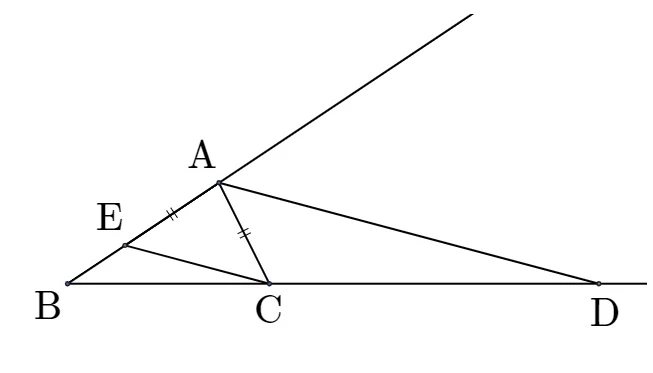
$\overline{\rm AE} = \overline{\rm AC}$ 인 $\rm E$를 잡으면, $\overline{\rm AB} : \overline{\rm AC} = \overline{\rm BD} : \overline{\rm CD}$이고 $\overline{\rm AB} : \overline{\rm AE} = \overline{\rm BD} : \overline{\rm CD}$이다. 삼각형의 닮음에 의해 $\overline{\rm AD} // \overline{\rm EC}$이다.
$\bigtriangleup \rm AEC$가 이등변 삼각형이므로 $\angle \rm AEC = \angle \rm ACE$이고, 삼각형의 외각에 의해 선분 $\rm AD$는 $\angle \rm BAC$의 외각의 이등분선이다.
'수학' 카테고리의 다른 글
| 사인법칙 알아보기(sin 법칙) (0) | 2022.11.19 |
|---|---|
| 파푸스의 중선정리 알아보기 (0) | 2022.11.18 |
| 삼각형의 내각의 이등분선 정리 (0) | 2022.11.16 |
| 사다리꼴의 중점연결정리 알아보기 (0) | 2022.11.16 |
| 삼각형의 중점연결정리 증명하기 (0) | 2022.11.15 |




댓글