반응형
삼각방정식의 일반해
1. sinx=a 이면 x=nπ+(−1)nα
2. cosx=a 이면 x=2nπ±α
3. tanx=a 이면 x=nπ+α
(단, α는 특수해, n은 임의의 정수)
삼각방정식의 풀이방법
1. 가능한 하나의 종류가 되도록 삼각방정식을 변형한 후 기본형으로 유도한다.
(ex sinx=a 형태) (sin2x+cos2x=1등의 삼각함수 공식들을 이용하기)
2. asinx+bcosx=c 형태의 방정식은 삼각함수의 합성공식을 이용해서 기본형으로 유도한다.
3. sinx=sinα, cosx=cosα, tanx=tanα의 형태의 방정식은 α를 하나의 특수해로 생각해서 계산한다.
4. 합 또는 차를 곱으로 이루어진 삼각방정식으로 변형한 후 방정식을 푼다.
728x90
'수학' 카테고리의 다른 글
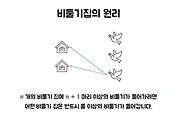
| 비둘기집의 원리와 응용방법 알아보기 (0) | 2023.01.20 |
|---|---|
| 드 무와브르 정리 알아보기 (0) | 2023.01.19 |
| 극한의 사칙연산과 부정형 극한값을 구하는 방법 (0) | 2023.01.17 |
| 소수 사이의 간격을 알 수 있는 소수정리 (0) | 2023.01.16 |
| 이항연산과 군의 정의, 군의 기본성질 알아보기 (0) | 2023.01.15 |
댓글