반응형
뉴욕의 맨해튼 거리는 많은 건물로 인해 이동하기가 쉽지 않다.
보편적인 A와 B의 거리가 A, B 직선 사이의 거리(유클리드 거리)이지만, 맨하튼 거리와 같이 건물들이 많다면, 직선으로 지나갈 수 없다. 건물을 가로지르지 않고 지나가야 하므로 다음 그림과 같은 형태로 이동하게 된다.
택시기하란 거리의 정의가 택시가 지나가는 경로와 유사하다고 해서 택시기하라 한다.

택시기하에서 A와 B의 거리는 길을 따라 길이를 더하는 것이다.
1. 유클리드 거리와 택시 거리의 비교


A, B의 위치가 같더라도, 두가지 정의가 다르기 때문에 그 값이 다르다.
즉 택시거리에서는 가로축, 세로축 값을 더하는 것이다.



2. 택시기하에서 삼각형

정삼각형의 정의가 세 변의 길이가 모두 같은 삼각형이라면, 유클리드 거리에서의 삼각형과 택시거리에서의 삼각형의 모양이 다르다. 위 그림과 같이 택시기하에서의 정삼각형은 이등변삼각형이다.
유클리드 거리에서 삼각형의 합동조건 3가지가 택시기하에서 성립하는지 알아보자.
1. 세 변의 길이가 같은 경우(SSS)
2. 두 변과 끼인각이 같은 경우(SAS)
3. 한 변과 양 끝각이 같은 경우(ASA)



합동은 겹쳤을 때, 완전하게 포개지는지 살펴보면 세가지 경우 모두 그림과 같이 겹칠 수 없다. 따라서 삼각형의 합동조건 3가지는 택시기하에서는 만족하지 않는다.
3. 택시기하에서 이차곡선



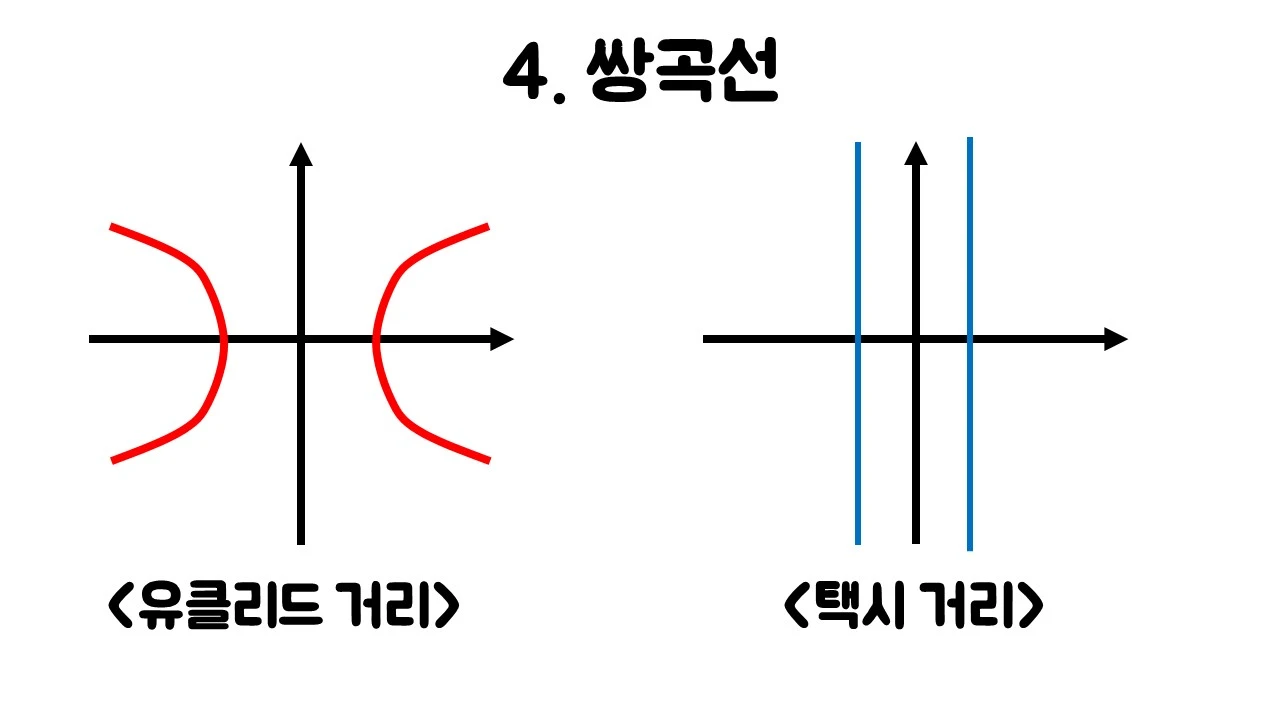
거리의 정의가 다르기 때문에 이차곡선의 형태가 모두 다르다.
728x90
'수학' 카테고리의 다른 글
| 3차방정식의 일반해 구하기(근의 공식) (1) | 2023.01.10 |
|---|---|
| 가우스 함수의 성질 알아보기 (0) | 2023.01.09 |
| 다각형의 내각의 합, 외각의 합 알아보기 (0) | 2023.01.07 |
| 정수 용어 정리 (0) | 2023.01.06 |
| 집합 용어 정리 (0) | 2023.01.05 |

댓글