복소수를 좌표평면 위의 점에 대응시켜 나타낼 수 있다. 이 때, 직교형식으로 나타내는 방법이 $z=a+bi \rightarrow A(a,b)$이다.
다음으로 복소수를 극형식으로 나타내는 방법을 알아보자.
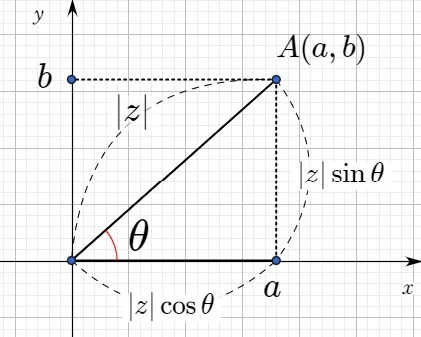
$z=a+bi$이고, 점을 직교좌표로 나타내면, $A(a,b)$이다. 선분 OA와 $x$축의 양의 방향과 이루는 각을 $\theta$라 하자.
이때 $a = |z|\cos \theta$, $b = |z|\sin \theta$ 이므로 이를 $z$에 대입하면, $z=|z|(\cos \theta + i \sin \theta)$ 이다. 이것이 복소수의 극형식이다.
또한 $\theta$를 $\arg(z) = \arg(a+bi)$라고 나타낼 수 있고, 이를 복소수의 편각이라고 한다.
복소수의 극형식
복소수 $z=a+bi$에서 $z$를 극형식으로 나타내면,
$z = r(\cos \theta + i \sin \theta)$ 이다. (단, $r = |z| = \sqrt{a^2+b^2}$, $\cos \theta = \frac{a}{r}$, $\sin \theta = \frac{b}{r}$ 이다.) 이때, $\tan \theta = \frac{b}{a}$ 이다.
복소수의 지수표현방법
$|z|=r$이고 편각이 $\theta$인 복소수는 $re^{i\theta}$로 나타낼 수 있다. 그 이유를 알아보자.
테일러 급수에 의해
$e^x = 1+\frac{1}{1!}x + \frac{1}{2!}x^2 + \frac{1}{3!}x^2 + \cdots $
$\sin x = x - \frac{1}{3!}x^3 + \frac{1}{5!}x^5 - \cdots $
$\cos x = 1 - \frac{1}{2!} x^2 +\frac{1}{4!}x^4 - \cdots $
로 나타낼 수 있다. $e^x$에서 $x = i \theta$를 대입하면,
$e^{i \theta} = 1+\frac{i\theta}{1!} + \frac{i^2\theta^2}{2!} + \frac{i^3\theta^3}{3!} + \frac{i^4\theta^4}{4!}+ \cdots $
$= 1+ \frac{\theta}{1!}i -\frac{\theta^2}{2!} -\frac{\theta^3}{3!}i +\frac{\theta^4}{4!} + \cdots $
$= (1-\frac{\theta^2}{2!} + \frac{\theta^4}{4!} - \cdots) + (\frac{\theta}{1!} - \frac{\theta^3}{3!} + \frac{\theta^5}{5!} - \cdots )i $
$= \cos \theta + i\sin \theta$
즉, $e^{i\theta} = \cos \theta + i \sin \theta$ 이다.
'수학' 카테고리의 다른 글
| 곱의 미분 증명하는 방법 (0) | 2022.12.04 |
|---|---|
| 몫(quotient)의 미분법 공식 증명하기 (0) | 2022.12.03 |
| 복소수, 복소평면 알아보기 (0) | 2022.12.01 |
| 부분분수 공식 모음(두개의 항, 세개의 항) (0) | 2022.11.30 |
| 중심각이 원주각의 두배인 이유 (0) | 2022.11.29 |
댓글