사인법칙은 삼각형에서 마주보는 변과 각, 그리고 외접원의 반지름 사이의 관계를 나타낸다.
사인법칙(sin 법칙)
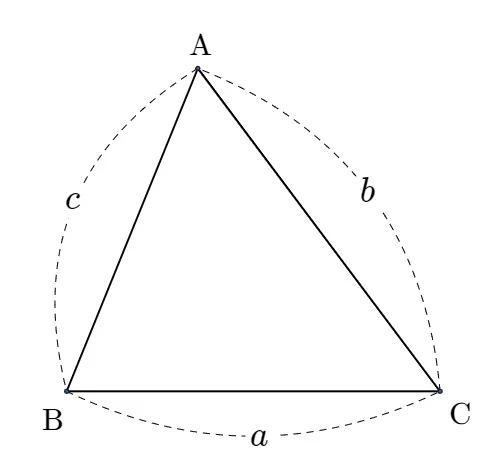
삼각형에서 마주보는 변과 각이 주어졌을 때, 다음 등식이 성립한다.
$\frac{a}{\sin \rm A} = \frac{b}{\sin \rm B} = \frac{c}{\sin \rm C} = 2R$
(예각, 직각, 둔각일 때 증명)
증명하기
(i) 직각삼각형일 때
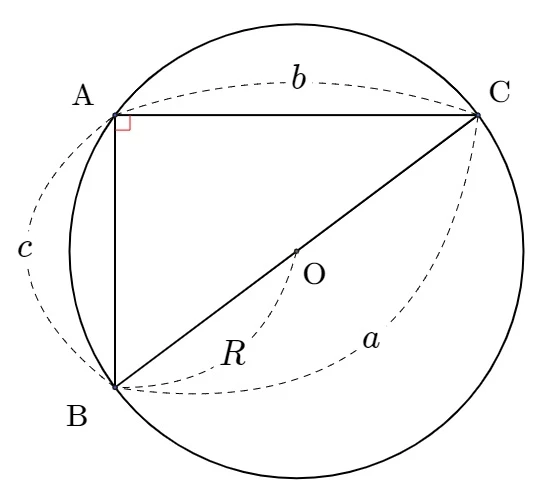
$\angle \rm A = 90^{\circ}$이므로 $\sin \rm A =1 $이다.
따라서 $a = 2R = \frac{a}{\sin \rm A}$ 가 성립한다.
(ii) 예각삼각형일 때
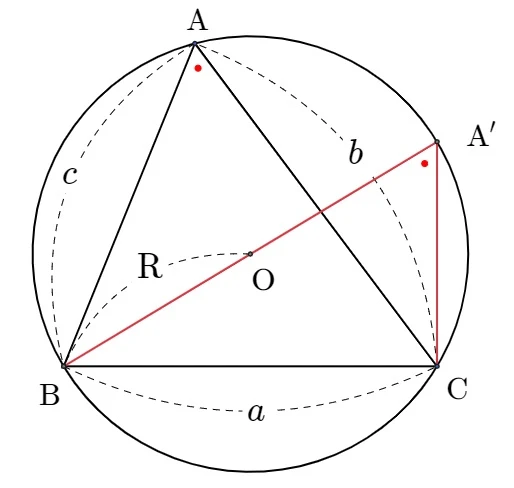
점 $\rm C$와 원의 중심을 연결하는 직선을 그을 때, 원과 만나는 $\rm C$가 아닌 점을 $\rm A'$라 하자. 이때 원주각의 성질에 의해 $\angle \rm BAC = \angle \rm BA'C$ 이다. 따라서 $\angle CBA' = 90^{\circ} $ 이고, 직각삼각형 $\rm BCA'$에서
$\sin \rm A = \sin \rm A' = \it \frac{a}{2R} $ 이다.
즉, $\frac{a}{\sin \rm A} = 2R$이 성립한다.
(iii) 둔각삼각형일 때
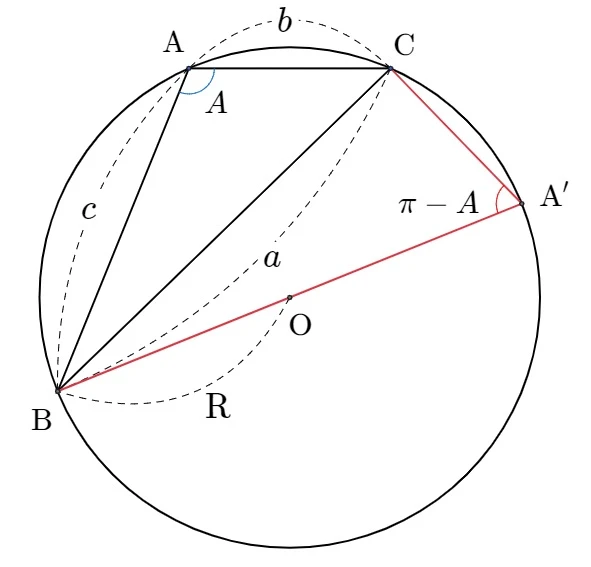
점 $\rm C$를 지나고 원의 중심을 지나는 직선을 그을 때, 원과 만나는 점을 $\rm A'$라 하자.
내접하는 사각형의 성질에 의해 $\angle \rm BCA' = \pi - A$ 이다.
따라서 $\angle \rm A'BC = 90^{\circ}$ 이고, 직각삼각형 $\rm BCA'$에서
$\sin \rm (\pi - a) = \it \frac{a}{2R}$이므로 $a = 2R \sin \rm A$이다.
즉, $\frac{a}{\sin \rm A} = 2R$이 성립한다.
제1코사인 법칙 알아보기
삼각형에 관한 법칙 중 제1, 2 코사인 법칙과 그 증명방법을 알아보자. 제1코사인법칙 $a=b \cos C + c \cos B$, $b=c \cos A + a \cos C$, $c=a\cos B + b \cos A$ 증명하기 1. 직각삼각형일 때, $a=b \cos C + c \cos B$에서
mathtravel.tistory.com
제2코사인법칙 알아보기
삼각형에서 두변과 그 끼인각이 주어진 경우 활용가능한 제2코사인법칙을 알아보자. 제2코사인법칙 $a^2 = b^2 + c^2 -2bc \cos A$ $b^2 = c^2 + a^2 -2ca \cos B$ $c^2 = a^2 + b^2 -2ab \cos C$ 증명하기 제1코사인법칙
mathtravel.tistory.com
'수학' 카테고리의 다른 글
| 제2코사인법칙 알아보기 (0) | 2022.11.19 |
|---|---|
| 제1코사인 법칙 알아보기 (0) | 2022.11.19 |
| 파푸스의 중선정리 알아보기 (0) | 2022.11.18 |
| 삼각형의 외각의 이등분선 정리 알아보기 (0) | 2022.11.18 |
| 삼각형의 내각의 이등분선 정리 (0) | 2022.11.16 |




댓글