타원 쌍곡선 접선 성질 모음

타원이란 두 초점과 같은 거리에 있는 점들의 집합이다. 이 타원 위의 점 P에서 접선을 그을 때 이 접선이 가지는 성질을 알아보자.

 

타원의 접선 성질 모음

1. 타원 위의 한 점 P에서 두 초점을 연결하는 선분을 그을 때, 빨간색 두 각의 크기는 서로 같다.

타원의 반사성질

 

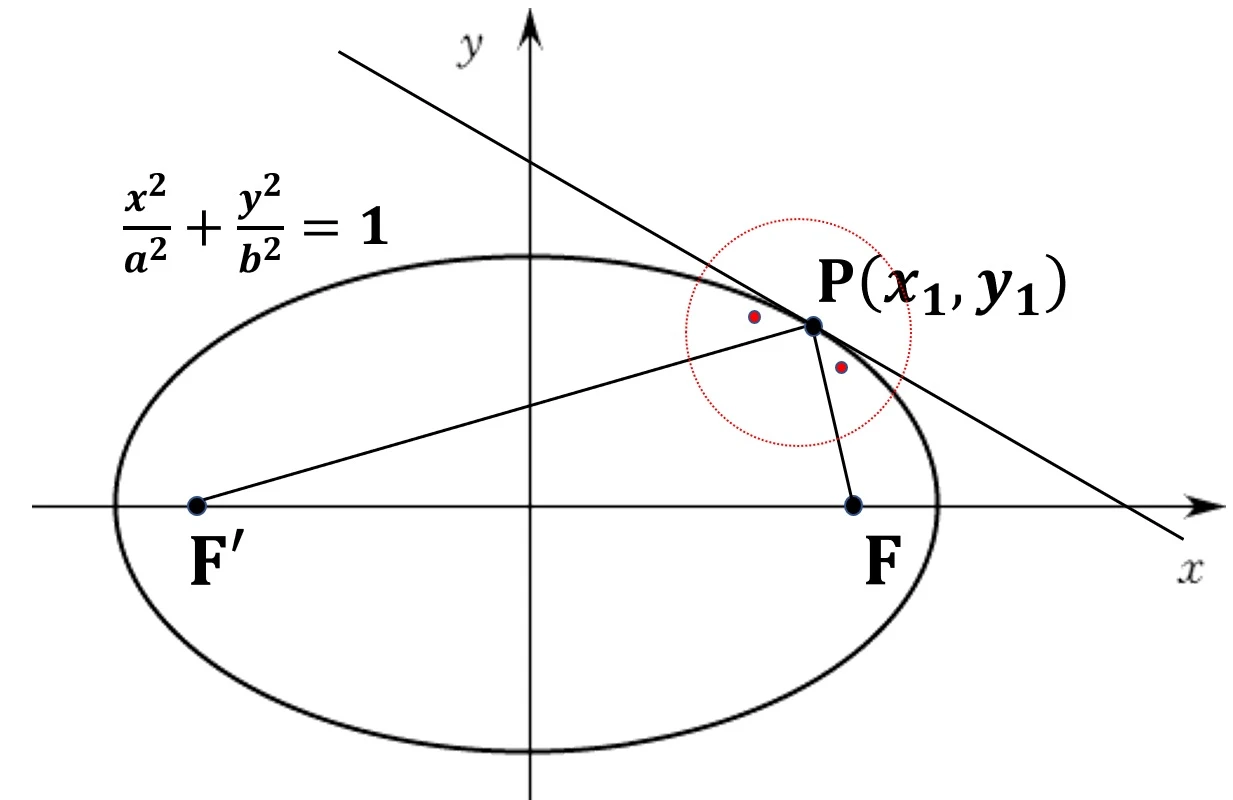
2. 타원 위의 한 점과 두 초점을 연결하는 선분을 그을 때, 점 P에서의 법선은 각을 이등분한다.

타원의 반사성질2

 

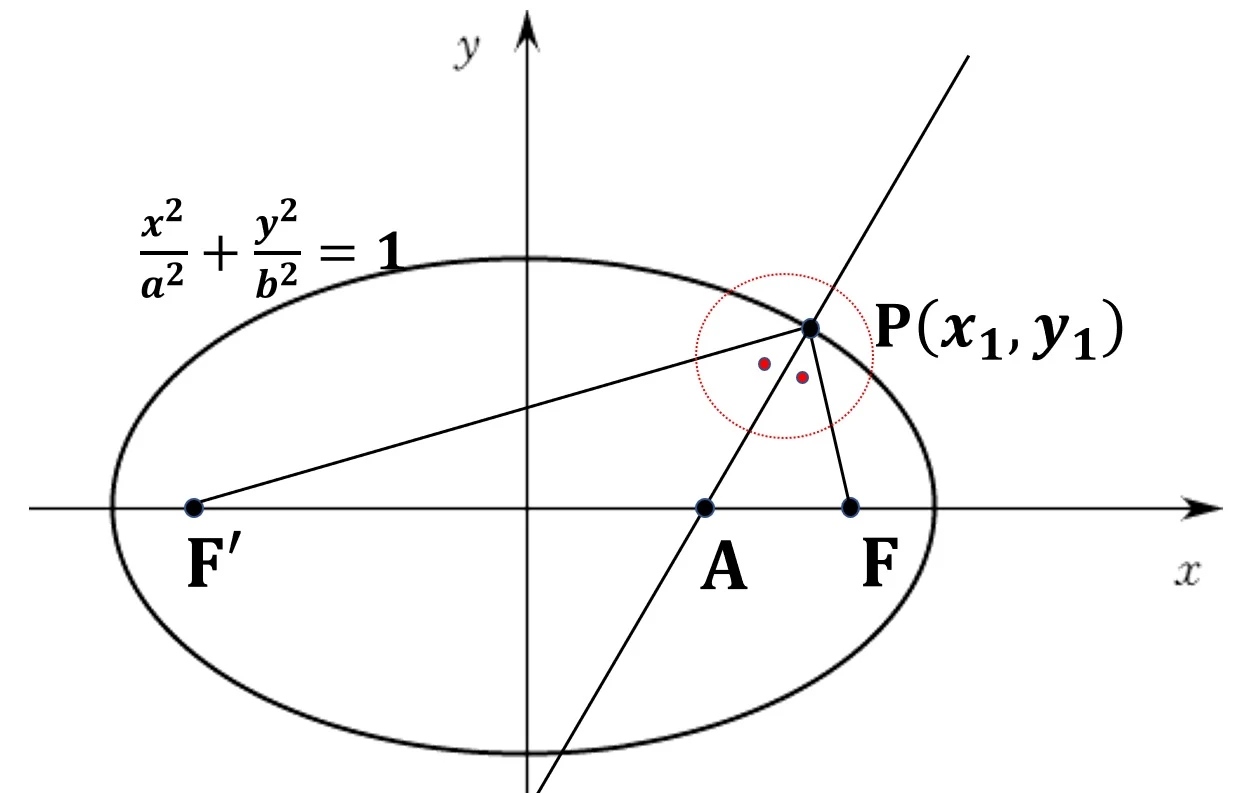
3. 타원 위의 한점에서 접선을 그을 때, 두 초점에서 내린 수선의 발은 모두 장축을 지름으로 하는 원 위에 있다.

장축을 지름으로 하는 원과의 관계

 

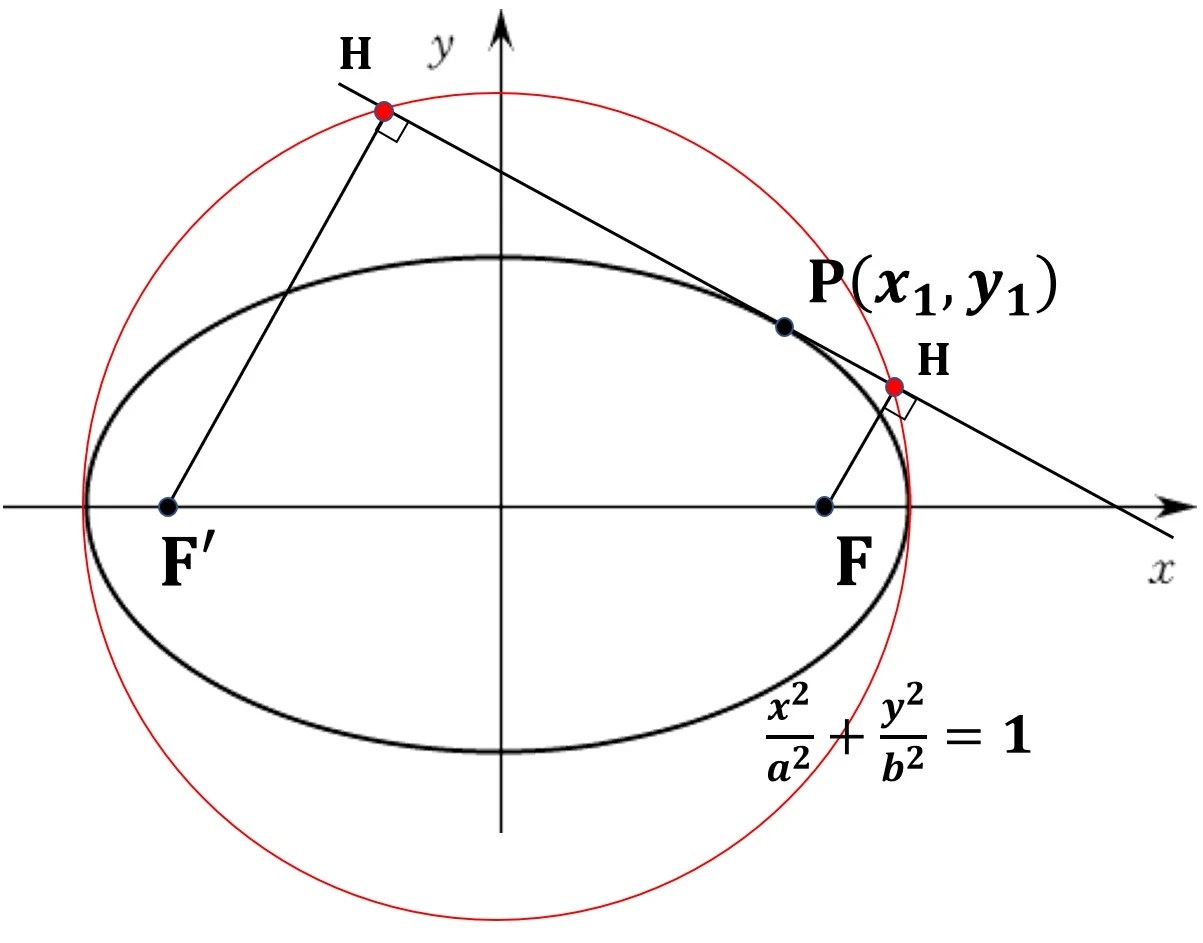
4. 타원 위의 한 점에서 접선을 그을 때, 접선의 x절편과 y절편을 각각 A, B라 하자. 한 점에서 x축과 y축에 내린 수선의 발을 C, D라 할 때, $\overline{OA} \cdot \overline{OC} = a^2$, $\overline{OB} \cdot \overline{OD} = b^2$ 을 만족한다.

접선을 그을때, 선분의 관계식

 

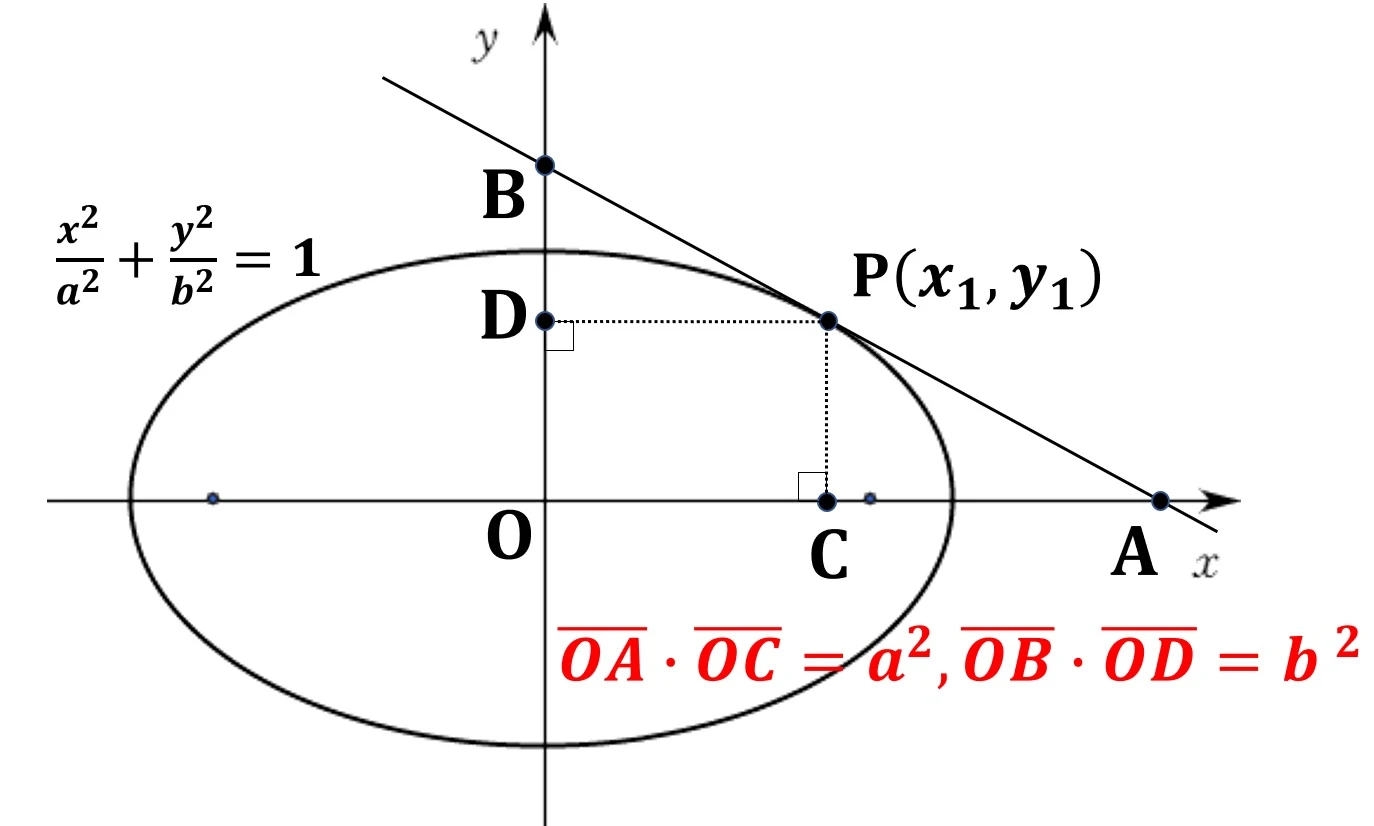
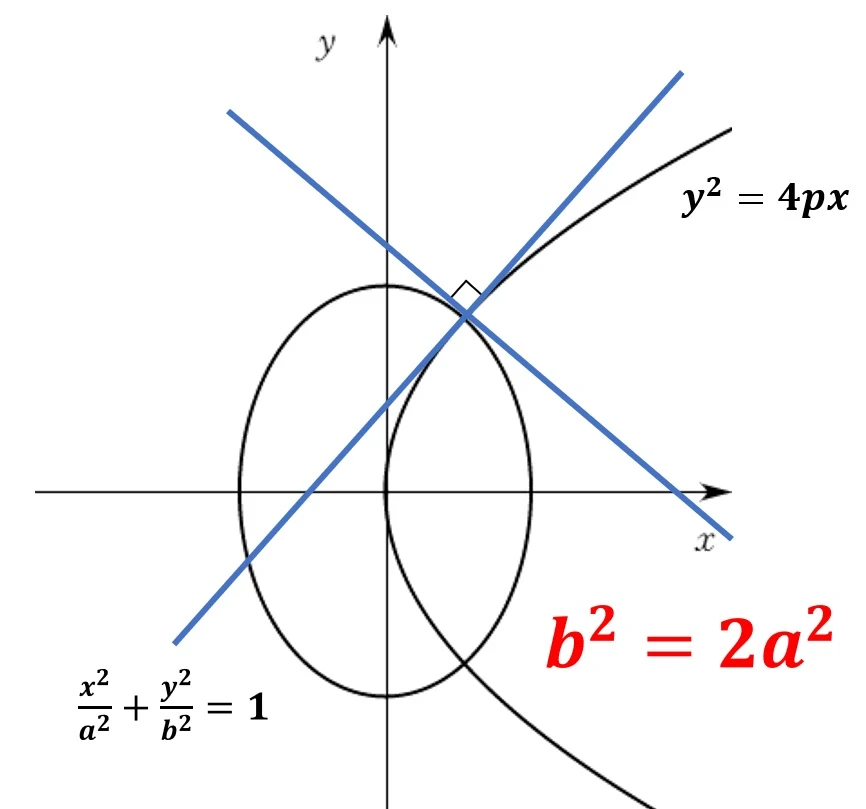
5. 포물선 $y^2 = 4px$와 타원 $\frac{x^2}{a^2} + \frac{y^2}{b^2}=1$이 직교하려면, $b^2 = 2a^2$이다.

포물선과 타원의 직교1

 

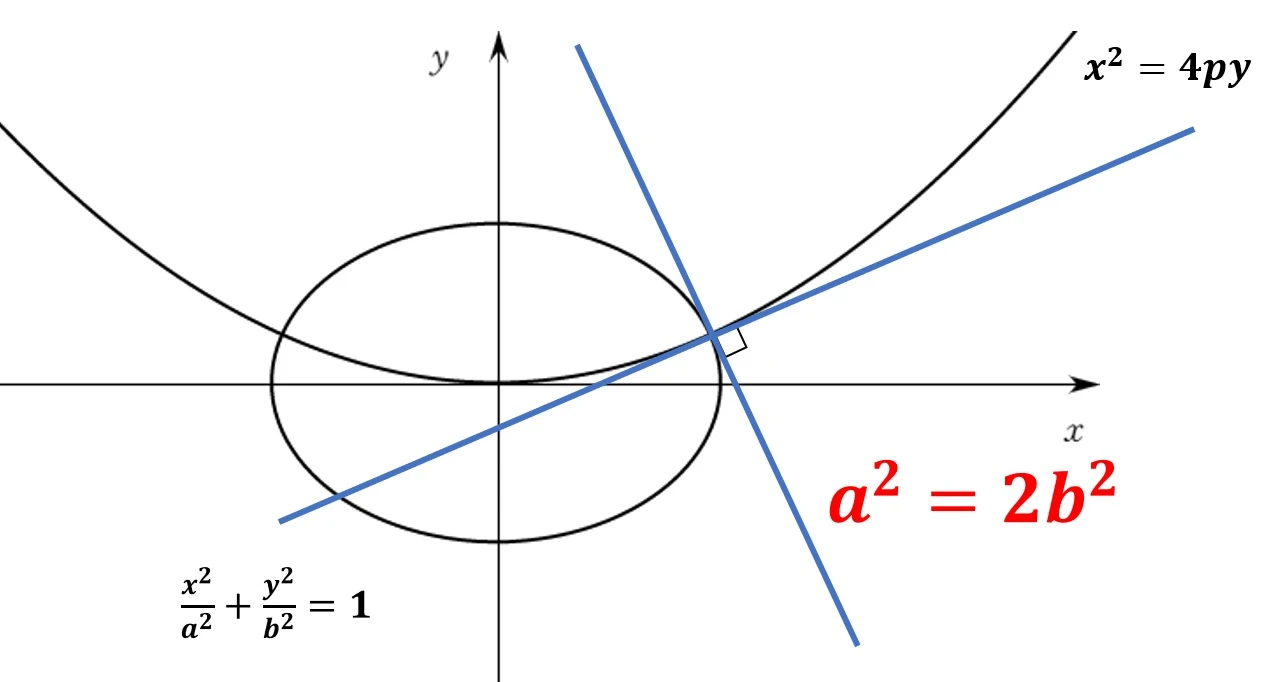
6. 포물선 $x^2 = 4py$와 타원 $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$이 직교하려면, $a^2 = 2b^2$이다.

포물선과 타원의 직교2

 

쌍곡선의 접선 성질 모음

쌍곡선이란 두 초점의 차가 일정한 점의 자취를 말한다. 쌍곡선 위의 한 점 P에서 접선을 그을 때, 만족하는 성질을 알아보자.

 

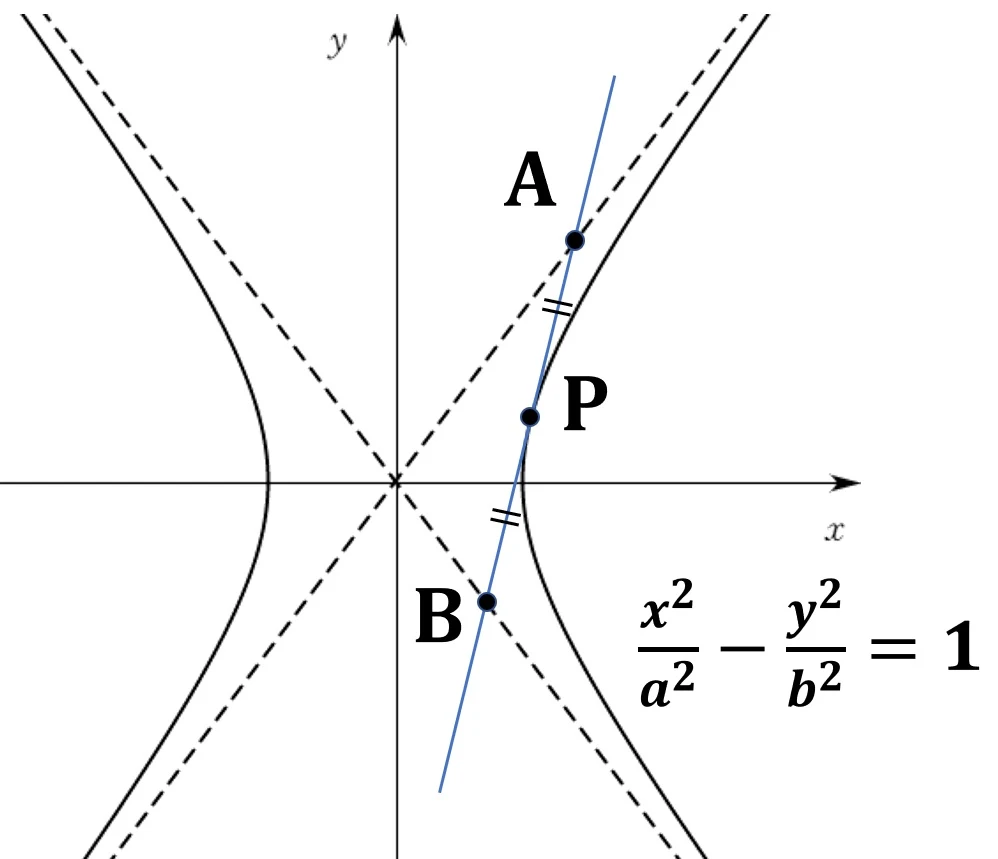
1. 쌍곡선 위의 점에서 접선과 두 점근선이 만나는 점을 A, B라 할때 접점은 선분 AB를 이등분한다.

접점 P는 선분 AB를 이등분한다.

 

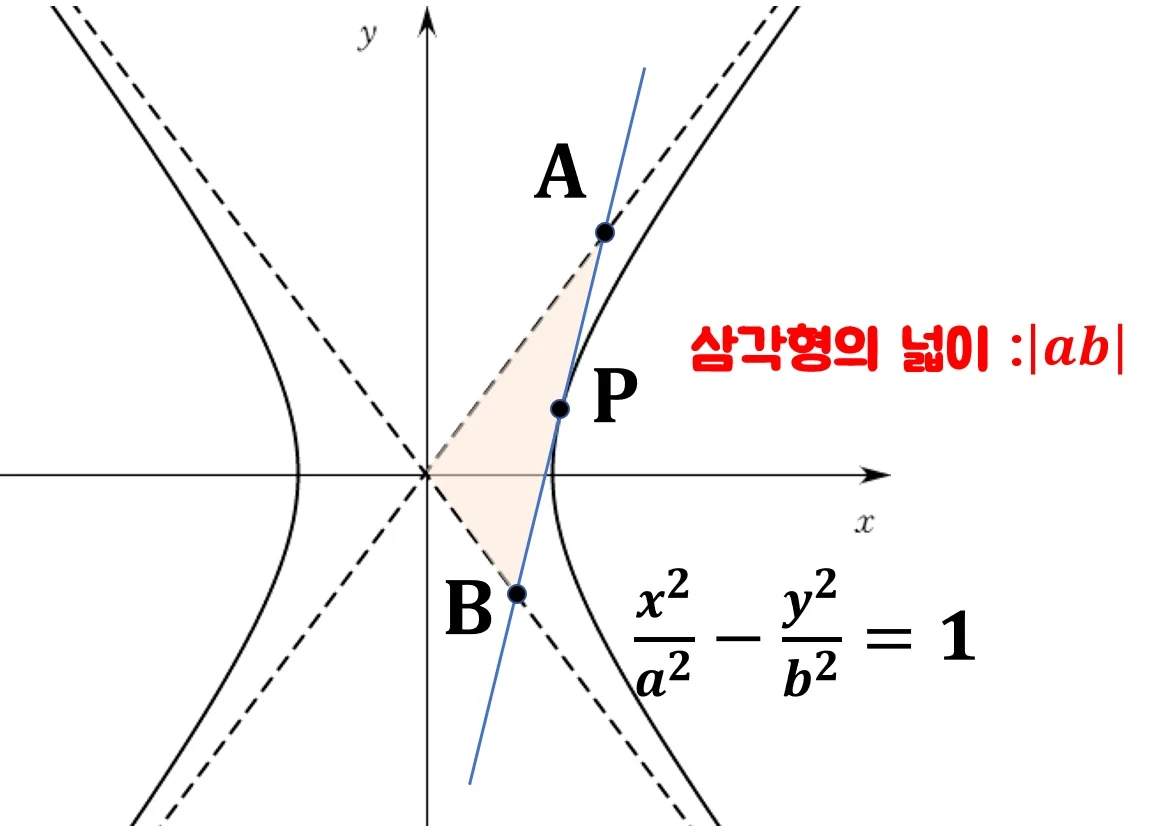
2. 쌍곡선의 접선과 두 점근선으로 이루어진 삼각형의 넓이는 $|ab|$로 일정하다.

그림의 삼각형 넓이는 일정하다.