두 개의 수를 기준으로 한 산술평균, 기하평균, 조화 평균은 다음과 같은 식을 갖는다.
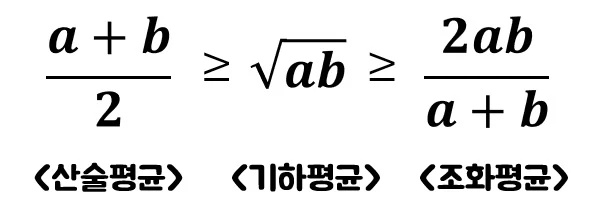
또한 이를 일반화시키면 아래와 같은 부등식을 얻을 수 있다.
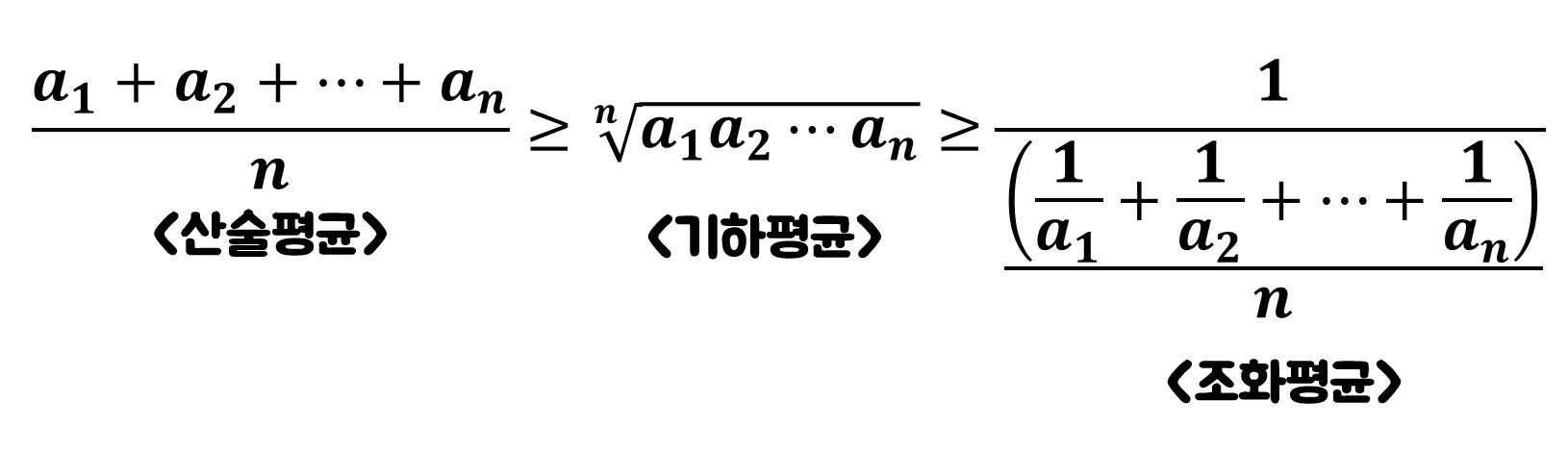
산술평균, 기하평균, 조화평균은 다음과 같은 대소 관계를 갖는다. 왜 이러한 대소 관계를 가지는지 기하학적, 대수적 방법 총 2가지로 증명해보자.
1. 기하학적 증명
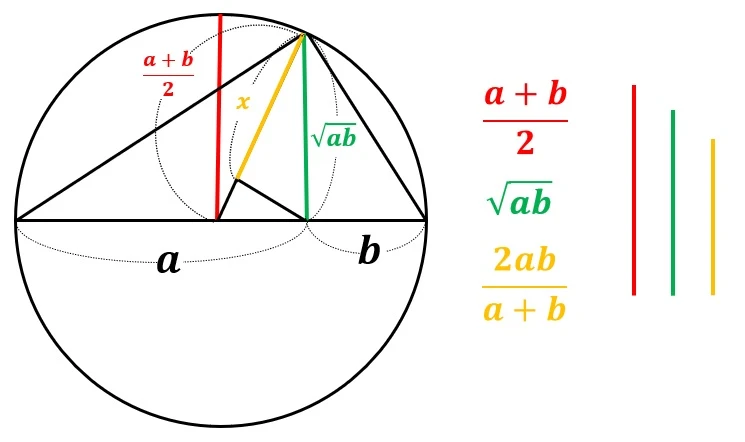
원을 그려서 반지름과 선분의 길이를 비교하면, 위 부등식을 쉽게 시각적으로 보일 수 있다.
2. 대수적인 증명
일반적인 식을 증명하기 위해 부등식을 부분으로 나누어 각각 증명해보자.
$\frac{a_1+a_2+ \cdots + a_n}{n} \geq \sqrt[n]{a_1a_2 \cdots a_n}$ 증명하기
(증명) 수학적 귀납법으로 증명하기
$n=2^1$일 때
$(\sqrt{a_1} - \sqrt{a_2})^2 \geq 0$이므로
$a_1 + a_2 -2\sqrt{a_1a_2} \geq 0$ ($a_1$, $a_2>0$)이다.
$\frac{a_1+a_2}{2} \geq \sqrt{a_1a_2}$ 이다.
따라서 $n=2^1$일 때 부등식이 성립한다.
$n=2^k$일때 부등식이 성립한다고 가정하면,
$\frac{a_1+a_2+ \cdots +a_{2^k}}{2^k} \geq \sqrt[2^k]{a_1a_2 \cdots a_{2^k}}$
양수 $a_1$, $a_2$, $\cdots$, $a_{2^{k+1}}$ 에서
$\frac{a_1+a_2 + \cdots + a_{2^{k+1}}}{2^{k+1}}=\frac{(a_1+a_2+ \cdots + a_{2^k})+(a_{2^k+1} +a_{2^k+2} +\cdots +a_{2^{k+1}} )}{2^{k+1}}$
$=\frac{1}{2} \{ \frac{a_1+a_2+ \cdots +a_{2^k}}{2^k}+ \frac{a_{2^k+1}a_{2^k+2}a_{2^{k+1}}}{2^k} \}$
$\geq \frac{\sqrt[2^k]{a_1a_2 \cdots a_{2^k}} \sqrt[2^k]{a_{2^k+1}a_{2^k+2} \cdots a_{2^{k+1}}}}{2} = \frac{\sqrt[2^k]{a_1a_2 \cdots a_{2^{k+1}}}}{2}$
$\geq \sqrt[2^{k+1}]{a_1a_2 \cdots a_{2^{k+1}}}$ 이다.
따라서 $n=2^{k+1}$일때 부등식이 성립한다.
이번에는 $n=k$일때 부등식이 성립한다고 가정하면,
양수 $a_1$, $a_2$, $\cdots$, $a_{2^{k+1}}$에서
$\frac{a_1+a_2+\cdots +a_{k-1}}{k-1} = \frac{\frac{k}{k-1} (a_1+a_2+\cdots +a_{k-1})}{k}$
$\frac{a_1+a_2+ \cdots +a_{k-1} + \frac{a_1+a_2+ \cdots +a_{k-1}}{k-1}}{k}$
$\geq \sqrt[k]{a_1a_2\cdots a_{k-1} ( \frac{a_1+a_2+ \cdots +a_{k-1}}{k-1} )}$
$\frac{a_1+a_2+ \cdots +a_{k-1}}{k-1} \geq \sqrt[k]{a_1a_2 \cdots a_{k-1} (\frac{a_1+a_2+\cdots +a_{k-1}}{k-1})}$
$(\frac{a_1+a_2+ \cdots +a_{k-1}}{k-1})^k \geq a_1a_2\cdots a_{k-1} (\frac{a_1+a_2+ \cdots + a_{k-1}}{k-1})$
$(\frac{a_1+a_2+ \cdots +a_{k-1}}{k-1})^{k-1} \geq a_1a_2 \cdots a_{k-1}$
$\frac{a_1+a_2 + \cdots a_{k-1}}{k-1} \geq \sqrt[k-1]{a_1a_2 \cdots a_{k-1}}$
따라서 $n=k-1$일때 부등식이 성립한다.
따라서 모든 자연수 $n$에 대해서 $\frac{a_1+a_2+ \cdots + a_n}{n} \geq \sqrt[n]{a_1a_2 \cdots a_n}$ 이 성립한다.
$\sqrt[n]{a_1a_2 \cdots a_n} \geq \frac{1}{\frac{(\frac{1}{a_1} + \frac{1}{a_2} + \frac{1}{a_3} + \cdots + \frac{1}{a_n})}{n}}$ 증명하기
산술평균, 기하평균 대소관계에 의해
$\frac{\sqrt[n]{\frac{a_1 \cdots a_n}{a_1^n} }+ \cdots + \sqrt[n]{\frac{a_1 \cdots a_n}{a_1^n}} }{n} \geq \sqrt[n]{\sqrt[n]{\frac{a_1 \cdots a_n}{a_1^n}} \cdots \sqrt[n]{\frac{a_1 \cdots a_n}{a_n^n}}} = \sqrt[n]{ \sqrt[n]{\frac{a_1^n \cdots a_n^n}{a_1^n \cdots a_n^n}} } = 1$ 이고,
$\frac{\sqrt[n]{\frac{a_1 \cdots a_n}{a_1^n}} + \cdots + \sqrt[n]{\frac{a_1 \cdots a_n}{a_n^n}} }{n}=\frac{\frac{\sqrt[n]{a_1 \cdots a_n}}{a_1} + \cdots + \frac{\sqrt[n]{a_1 \cdots a_n}}{a_n}}{n}= \sqrt[n]{a_1 \cdots a_n} \times \frac{(\frac{1}{a_1} + \frac{1}{a_2} + \cdots + \frac{1}{a_n})}{n} \geq 1$
따라서 $\sqrt[n]{a_1a_2 \cdots a_n} \geq \frac{1}{\frac{(\frac{1}{a_n} + \frac{1}{a_2} + \cdots +\frac{1}{a_n} )}{n}}$
가 성립한다.
$\therefore \frac{a_1+a_2+a_3+ \cdots + a_n}{n} \geq \sqrt[n]{a_1a_2 \cdots a_n} \geq \frac{1}{\frac{(\frac{1}{a_1} + \frac{1}{a_2} + \frac{1}{a_3} + \cdots + \frac{1}{a_n})}{n}} $
'수학' 카테고리의 다른 글
| 중심각이 원주각의 두배인 이유 (0) | 2022.11.29 |
|---|---|
| 삼각형의 내심, 외심 알아보기 (0) | 2022.11.28 |
| 산술평균, 기하평균, 조화평균 알아보기 (0) | 2022.11.26 |
| 메르센 소수, 페르마 소수 알아보기 (0) | 2022.11.25 |
| 이차곡선 공식 정리(이차곡선 공식모음) (0) | 2022.11.24 |




댓글